Capítol 3: Operacions de nombres binaris al microprocessador
3.1 Introducció
En un ordinador, les operacions aritmètiques es fan en 8 bits, 16 bits, 32 bits o 64 bits. Un nombre com el 3 en binari és 11. Si l'operació s'ha de fer en 8 bits, es considera 00000011; precedint-lo amb 0 zeros.
Per a un nombre binari com 10000101, el bit més significatiu és el bit de l'extrema esquerra. És 1 en aquest cas. El bit menys significatiu és el bit extrem de la dreta, que encara és 1, per al nombre. El bit més significatiu s'abreuja com a MSB. El bit menys significatiu s'abreuja com a LSB.
El dígit BINARI s'abreuja com a BIT i simplement s'escriu com a bit. En el número 10010011, cada un o zero és una mica. Un grup de quatre bits s'anomena nibble. Un grup de vuit bits s'anomena byte. Un byte consta de dos mordiscos. El mosseig inferior és el mosseig per a l'LSB i el mossegut més alt és el mossegada per a l'MSB.
Un grup de 8 bits, 16 bits, 32 bits o 64 bits s'anomena paraula, sempre que aquest grup transmeti informació més enllà d'indicar un nombre. El grup s'anomena paraula, per exemple, si és una instrucció de baix nivell a l'ordinador. També hi ha una paraula de 24 bits, però avui no s'utilitza habitualment.
Endianness es refereix a l'ordre en què els bytes formen una paraula. Considereu la paraula de 24 bits: 100100001111010100100010. Aquesta paraula consta de tres bytes que són:
10010000 11110101 00100010
El byte més significatiu és el byte més esquerre. Quan el byte de l'extrema esquerra és el byte més significatiu i el de l'extrema dreta és el byte menys significatiu, això s'anomena representació Big Endian de la paraula. La representació de Little Endian és el contrari.
La memòria de l'ordinador és una sèrie de cel·les, i cada cel·la conté un byte. La primera cel·la de la memòria de l'ordinador és per al byte 0, la segona és per al byte 1, la tercera és per al byte 2, i així successivament. Amb gran endianitat i per a la paraula anterior, el byte més significatiu s'emmagatzema a la cel·la byte 0, el byte mitjà s'emmagatzema a la cel·la byte 1 i el byte menys significatiu s'emmagatzema a la cel·la byte 2. Això vol dir que hi ha bytes més significatius a la cel·la de memòria inferior.
La paraula anterior de 24 bits es pot escriure en ordre invers de bytes de la següent manera:
00100010 11110101 10010000
Ara, el byte menys significatiu es troba a l'extrema esquerra i el byte més significatiu es troba a l'extrema dreta. Quan el byte de l'extrema esquerra és el byte menys significatiu i el byte de l'extrema dreta és el byte més significatiu, és la representació Little Endian de la paraula. Amb poca endianitat i per a la paraula anterior, el byte menys significatiu s'emmagatzema a la cel·la byte 0, el byte mitjà s'emmagatzema a la cel·la byte 1 i el byte més significatiu s'emmagatzema a la cel·la byte 2. Això vol dir que hi ha un byte menys significatiu a la cel·la de memòria inferior.
Endianness no s'utilitza per als bits d'un byte. Tampoc s'utilitza per a picades en un byte. Només s'utilitza per a l'ordre de bytes.
La recta numèrica
Un nombre sense signe és un nombre positiu. Els nombres positius són nombres de zero que van cap amunt. També existeixen nombres negatius. Els nombres positius i negatius es poden presentar en una recta numèrica. La següent línia numèrica mostra els nombres enters positius i negatius (ners) propers a zero:
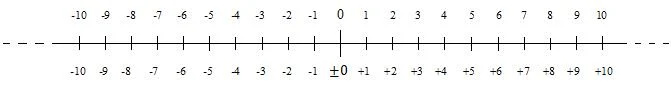
Els nombres negatius disminueixen de zero cap avall (cap a l'esquerra). En moltes situacions, zero es considera positiu. Tanmateix, es considera negatiu en algunes situacions. Per això hi ha un signe més i menys davant del zero, a la numeració inferior, al diagrama. Quan un nombre és positiu, es pot ometre el seu signe; aquest és el cas de la numeració superior del diagrama. El signe menys davant d'un nombre negatiu mai s'omet.
3.2 Suma de nombres binaris
A més a més:
A + B = S
A s'anomena augend, B s'anomena sumand i S s'anomena suma.
Considereu la següent suma de dos nombres positius en base dos:

A la base dos, els únics dígits possibles són 0 i 1. La suma a la base 2 és semblant a la suma a la base deu, però dos a la base dos és un zero (10). Quan la suma de dos bits en una columna és 10, s'escriu 0 i 1 es porta a la columna esquerra immediata; s'ha de sumar a la suma dels dos bits que hi ha. Quan la suma total és tres, significa 11 a la base dos. S'escriu l'1 dret entre 11 i l'1 esquerre es porta per afegir-lo a la suma dels bits de la columna esquerra immediata. En qualsevol cas, l'1 portat cap a l'esquerra s'anomena portar.
Llegint la taula d'addicions anterior des de la dreta, a la segona columna (des de la dreta), hi ha un acarreament que resulta de 1+1 = 10. A la tercera columna, hi ha un acarreament que resulta de 1+1+ acarreament de 1 = 11. A la quarta columna, hi ha un carry que resulta de 0+1+ carry d'1 = 10. A la cinquena columna, no hi ha cap carry perquè la suma és 0+0+ carry d'1 = 1. El la resta de columnes no implica portar.
El recompte de columnes comença des de l'extrem dret. Amb l'addició de 16 bits, pot haver-hi una transferència de la vuitena columna a la novena columna (movint-se cap a l'esquerra). La taula següent ho il·lustra:

Les operacions aritmètiques i lògiques tenen lloc al microprocessador de la placa base de l'ordinador.
Per a un ordinador de paraules de 8 bits, el transport no pot passar del vuitè bit al novè bit automàticament per maquinari. Per tant, per afegir dos grups de 16 bits en aquest ordinador, l'addició s'ha de fer dues vegades en parells de vuit-vuit bits. El transport és mogut i realitzat pel programari (programació).
Per afegir dos nombres, els nombres es poden convertir primer a la seva forma de complement a dos (vegeu més avall) abans d'afegir-los.
3.3 El complement de dos i la seva resta de nombres binaris
A la placa base de l'ordinador, hi ha la memòria i hi ha el microprocessador i altres circuits. La memòria és una sèrie de cel·les de vuit bits. Per a un byte, cada bit entra a una cel·la. El microprocessador té unes quantes ubicacions de tipus de memòria. Aquestes ubicacions de tipus de memòria s'anomenen registres. Així, a l'ordinador, els grups de bytes es poden emmagatzemar temporalment a la memòria o als registres del microprocessador.
En qualsevol d'aquests emmagatzematges, cada cel·la pot prendre un 1 o un 0, i res més. A la vida hi ha números positius i negatius. Un nombre positiu comença amb un signe més (+) i un nombre negatiu comença amb un signe negatiu (-). Quan s'omet el signe, el nombre es considera un nombre positiu.
Per tal de resoldre aquest problema d'indicar el signe d'un nombre a l'ordinador, els nombres sencers s'emmagatzemen en rangs. Els nombres enters són nombres enters. Si s'utilitzen vuit bits per emmagatzemar el rang de nombres possibles, el bit més esquerre s'utilitza com a bit de signe. Si el nombre comença per 0, el nombre és un nombre positiu. Si comença per 1, el nombre és un nombre negatiu. Si s'utilitzen setze bits per emmagatzemar el rang de nombres possibles, el bit més esquerre s'utilitza com a bit de signe. Si el nombre comença per 0, t el nombre és un nombre positiu. Si comença per 1, el nombre és un nombre negatiu. Els números d'aquest formulari s'anomenen números signats.
A la pràctica, hi pot haver números signats per a 8 bits, 16 bits, 32 bits i 64 bits. Com més ampli sigui el nombre de bits utilitzats, més gran serà el rang de possibles números que es poden emmagatzemar.
Nombres enters de complement a dos
Amb el complement de dos, els nombres positius són els nombres de recompte normals, excepte que el dígit més a l'esquerra és 0. Per obtenir el nombre negatiu corresponent per a qualsevol nombre positiu donat, inverteix cada bit del nombre i afegeix 1 al resultat. L'invertit o complement de 0 és 1. L'invertit o complement d'1 és 0. Les taules següents mostren alguns nombres de complement a dos en els seus rangs:
| Taula 3.31 Nombres enters de complement a dos en dos bits |
|
|---|---|
| Binari | Decimal |
| 01 | +1 |
| 00 | +0 |
| 11 | -1 |
| 10 | -2 |
Els nombres binaris positius són 00 i 01 (és a dir, zero i un). Al bit més esquerre, zero indica que són nombres positius. 00 és una mica al mig del rang. Per obtenir -1, es troba que la inversió del nombre 01 és 10. Sumant 1 a això (a l'extrema dreta) s'obté 11.
Com que s'utilitzen dos bits, només queda un bit per representar els nombres de l'interval que consta dels números +1, +0 i -1 corresponents a 01, 00 i 11. El primer bit indica el signe. Succeeix que 10 per +2 no es troba entre aquests tres nombres binaris. 10 comença amb 1, la qual cosa significa que ha de ser un nombre negatiu en el complement de dos. Per tant, 10 s'inclou a l'interval, per significar -2.
Amb dos bits en el complement de dos, el nombre de tots els nombres enters (positius i negatius) que es poden representar és 2 2 = 4 i no 2 2 -1 = 3. El matís resulta de la inclusió de l'últim nombre negatiu que és el negatiu de 2 nombreamb – 1. En aquest cas, -2 2-1 = -2 1 = -2. No hi ha +2 en el rang de nombres de complement a dos en 2 bits.
| Taula 3.32 Nombres enters de complement a dos en quatre bits |
|
|---|---|
| Binari | Decimal |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
Els nombres binaris positius van del 0000 al 0111 (és a dir, del zero al set). Al bit més esquerre, zero indica que són nombres positius. 0000 és una mica al mig del rang. Per obtenir -1, es troba que la inversió del nombre 0001 és 1110. Si afegim 1 a això (a l'extrema dreta) s'obté 1111. Per obtenir -2, es troba que la inversió de 0010 és 1101. Afegint 1 a això ( de l'extrema dreta) dóna 1110. Els altres nombres binaris negatius com -3 a -7 es determinen de la mateixa manera.
Com que s'utilitzen quatre bits, en queden tres per representar els nombres de l'interval que són +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 i -7 corresponents a 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1010, i 10101, i 1010
El -8 que correspon a 1000 s'ha d'adreçar per separat. El primer bit de tots aquests nombres indica el signe de 0 per a nombres positius i 1 per a nombres negatius. Passa que 1000 no es troba entre aquests catorze nombres binaris. 1000 comença amb 1, la qual cosa significa que ha de ser un nombre negatiu, pel que fa al complement de dos. Per tant, 1000 s'inclou a l'interval, per significar -8.
Amb quatre bits en complement de dos, el nombre de tots els nombres enters (positius i negatius) que es poden representar és 2 4 = 16 i no 2 4 – 1 = 15. El matís resulta de la inclusió de l'últim nombre negatiu que és el negatiu de 2 numberWidth – 1. En aquest cas, -2 4 -1 = -2 3 = -8. No hi ha +8 en el rang de nombres.
L'anàlisi anterior de dos, quatre i bits més amples en el complement de dos es pot aplicar a nombres binaris de 8 bits, 16 bits, 32 bits i 64 bits d'ample.
El complement a dos sacrifica el primer bit (l'extrem esquerre) pel signe de 0 per al nombre positiu i 1 per al nombre negatiu. Per al grup de bits ample 'n' bits, n'hi ha 2 n nombres totals positius més negatius. Seria 2 n -1, si no fos pel darrer nombre negatiu (el més petit) de la sort inclòs. El nombre positiu més alt és +2 n-1 -1 i el nombre negatiu més petit és -2 n-1 -1. Seria -2 n-1 -1, si no fos pels afortunats -2 n-1 inclòs.
Resta de nombres en el complement de dos
En resta:
A-B = D
A s'anomena minuend, B s'anomena subtrahend i D s'anomena diferència.
Per restar un nombre binari positiu d'un altre nombre binari positiu, el minuend s'escriu en complement a dos i el subtrahend es converteix en el seu valor de complement a dos negatiu. Així, l'enunciat matemàtic esdevé:
A+ – B = D
En altres paraules, en la resta del complement a dos, el subtrahend es converteix en un nombre negatiu i després s'afegeix al minuend.
Exemple 3.31:
Avalueu la següent expressió decimal en complement de dos utilitzant quatre bits:
6 – 4
Solució:
El nombre binari de 6 és 110. En el complement a dos de 4 bits, és 0110. El nombre binari de +4 és 100. En el complement a dos de 4 bits, és 0100. 0100 que s'ha de convertir en negatiu 4 en dos. complement de la següent manera: El complement o inversió de 0100 és 1011. Si afegim 1 a això des de l'extrem dret, com hem fet a més, dóna 1100. Per tant, l'expressió decimal és:
6 – 4 que es converteix en:
0110 – 0100 que és
0110 +(– 0100) = 0110 + 1100 fet com a la secció d'addició anterior com:

Nota: 0110 +(– 0100) és el mateix que 6 + – 4
Amb la resta del complement a dos, qualsevol arrastre, després de l'última columna cap a l'esquerra, a la suma, es llença. En restar en decimal, l'enunciat matemàtic és:
6 – 4 = 2
Fent el mateix en el complement a dos, la resposta és 0010, que és +2 en el recompte binari del complement a dos. La resta anterior resta un nombre més petit d'un nombre més gran. En l'exemple següent, un nombre més gran es resta d'un nombre més petit. Es pot consultar la taula 3.32 per veure si 0010 és realment el complement de dos que equival a +2.
Exemple 3.32:
Avalueu la següent expressió decimal en complement de dos amb quatre bits:
4 – 6
Solució:
El nombre binari de 4 és 100. En el complement a dos de 4 bits, és 0100. El nombre binari de +6 és 110. En el complement a dos de 4 bits, és 0110. 0110 s'ha de convertir en 6 negatiu en el complement de dos de la següent manera: El complement o inversió de 0110 és 1001. Si afegim 1 a això des de l'extrem dret, com vam fer a l'addició anterior, s'obté 1010. Per tant, l'expressió decimal és:
4 – 6 que es converteix en:
0100 – 0110 que és
0100 +(– 0110) = 0100 + 1010 fet com a la secció d'addició anterior com:

Nota: 4+ – 6 és el mateix que 0100 +(– 0110).
Amb la resta del complement a dos, qualsevol arrastre, després de l'última columna cap a l'esquerra, a la suma, es llença. En restar en decimal, l'enunciat matemàtic és:
4 – 6 = -2
Fent el mateix en el complement a dos, la resposta és 1110, que és -2 en el recompte binari del complement a dos. Es pot consultar la taula 3.32 per veure si 1110 és realment el complement de dos que equival a -2.
3.4 Multiplicació de nombres binaris
En el comunicat:
A x B = P
A s'anomena multiplicand, B s'anomena multiplicador i P s'anomena producte. L'expressió A x B significa sumar A, B el nombre de vegades que A i B són nombres enters (nombres sencers).
La multiplicació en binari és el mateix que la multiplicació en decimal. Tanmateix, en comptes de fer-ho en decimal, es fa en binari. La multiplicació de l'expressió decimal de 42 x 10 es fa en binari de la següent manera on 42 10 = 101010 2 i 10 10 = 1010 2 :
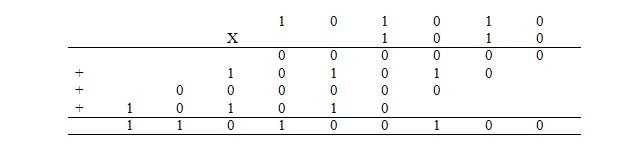
Els 4 nombres que s'afegeixen s'anomenen productes parcials. La resposta és el producte. L'addició dels productes parcials es fa de la mateixa manera que s'ha explicat anteriorment.
La multiplicació també es pot veure de la següent manera: En aquesta multiplicació de base dos, si el bit (dígit) del multiplicador és 1, el bit menys significatiu del seu producte parcial és el bit menys significatiu del multiplicand que es torna a escriure directament sota ell; i la resta de bits del multiplicant es repeteixen cap a l'esquerra. En aquesta multiplicació de base dos, si el bit (dígit) del multiplicador és 0, el seu producte parcial consta de zeros amb el bit menys significatiu de 0 directament a sota. El nombre de tots els zeros és el nombre de bits del multiplicand.
3.5 Divisió de nombres binaris
En el comunicat:
A ÷ B = Q
A s'anomena dividend, B s'anomena divisor i P s'anomena quocient. El quocient pot anar acompanyat d'un residu. L'expressió A ÷ B significa quantes vegades es pot afegir B per donar A o estar a prop d'ella de manera que la resta sigui 0 o menor que B.
La divisió es pot fer de moltes maneres. La divisió que es mostra aquí és la divisió de restauració.
Divisió de restauració
Aquest és el mètode de divisió llarga que s'aprèn a les escoles. Si 237 es divideix per 6, la resposta és 39 resta 3. El 237 10 a la base 2 és 11101101 2 i 6 10 a la base 2 és 110 2 . El 39 10 a la base 2 és 100111 2 i 3 10 a la base 2 és 11 2 .
Així, 11101101 2 dividit per 110 2 dóna 100111 2 resta 11 2 a la base dos. Amb el mètode de restauració, els nombres binaris són nombres ordinaris i no estan necessàriament en complement de dos. L'estructura següent divideix 11101101 2 al 110 2 donar 100111 2 resta 11 2 :

La resta es fa de manera ordinària i no utilitzant el complement de dos. Com que aquesta és la base dos, un préstec és dos i no deu. Els dividends parcials són 10, 101, 1011, 1010 i 1001. 11 és la resta. Com que el divisor té tres dígits, la divisió es fa bàsicament en grups de tres dígits a partir del dividend donat. El quocient és el nombre sencer (enter) i és 100111 per a aquest problema. El resultat del quocient i la resta és el que s'esperava.
3.6 Operacions aritmètiques amb programari i maquinari
La placa base de l'ordinador té un rellotge. Els tic-tacs del rellotge s'anomenen polsos. A cada pols de rellotge, es prenen una o més decisions en diferents llocs de la placa base; i això té a veure amb la programació (programari).
Dins del microprocessador, hi ha dos tipus de circuits anomenats: Circuits lògics combinacionals i Circuits lògics seqüencials. Hi ha un altre tipus de circuit anomenat multiplexor. La suma, la multiplicació i la divisió poden tenir lloc dins d'un interval de rellotge mitjançant la lògica combinacional (circuit). Mentre que la programació (programari) compromet la decisió a cada pols de rellotge utilitzant els circuits lògics seqüencials i els multiplexors.
Quan es fa la resta amb el complement a dos, calen almenys dos polsos de rellotge. Al primer pols de rellotge, un multiplexor canalitza el subtrahend a un conjunt de portes NOT (una porta NOT per dígit). Al segon pols de rellotge, la lògica combinacional afegeix 1 a la sortida de les portes NOT i continua afegint el subtrahend i el minuend resultants. Tota aquesta suma pot tenir lloc en un interval de rellotge.
La suma, la multiplicació i la divisió encara es poden reduir amb la programació utilitzant les taules de veritat. Tanmateix, no es tracta en aquest curs de carrera en línia.
3.7 Operacions lògiques en el microprocessador
AND, OR, XOR i Invert
I
La taula següent il·lustra el AND bit a bit. Això vol dir que per a dos nombres binaris diferents, els bits corresponents són AND basats en la taula de veritat AND:
Mou-se d'esquerra a dreta, 1 I 1 = 1; 0 I 1 = 0; 0 I 0 = 0; 1 I 0 = 0; i així successivament d'acord amb la taula de veritat AND.
O
La taula següent il·lustra l'OR bit a bit. Això vol dir que per a dos nombres binaris diferents, els bits corresponents són OR basats en la taula de veritat OR:

Moure's d'esquerra a dreta, 1 O 1 = 1; 0 O 1 = 1; 0 O 0 = 0; 1 O 0 = 1; i així successivament d'acord amb la Taula de Veritat OR.
GRATIS
La taula següent il·lustra l'OR exclusiu de bits. Això vol dir que per a dos nombres binaris diferents, els bits corresponents són XOR basats en la taula de veritat XOR:

Mou-se d'esquerra a dreta, 1 XOR 1 = 0; 0 XOR 1 = 1; 0 XOR 0 = 0; 1 XOR 0 = 1; i així successivament d'acord amb la taula de veritat XOR.
Inverteix (NO)
La taula següent il·lustra el NO bit a bit (invertir). Això vol dir que per a un nombre binari, aquesta vegada, cada bit s'inverteix en funció de la taula de veritat NOT:

Moure's d'esquerra a dreta, NO 1 = 0; NO 0 = 1; NO 0 = 1; NO 1 = 0; i així successivament d'acord amb la Taula de Veritat NO.
Canvi a la dreta o a l'esquerra
Canvia a la dreta
El número binari següent es desplaça 3 posicions de bits a la dreta, amb els zeros inserits a les posicions de bits desocupades a l'esquerra:

El desplaçament es pot fer per a una, dues, tres, quatre places, etc.
Canvi a l'esquerra
El número binari següent es desplaça 3 posicions de bits a l'esquerra, amb els zeros inserits a les posicions de bits desocupades a la dreta:

El desplaçament es pot fer per a una, dues, tres, quatre places, etc.
Gira a la dreta o a l'esquerra
Girar és similar al desplaçament. Es fa una mica a la vegada. En girar cap a la dreta, els bits que surten de l'extrem dret no cauen com en el desplaçament; substitueixen els bits buits de l'esquerra, un per un. En girar cap a l'esquerra, els bits que surten de l'extrem esquerre no cauen com en el desplaçament; substitueixen els bits buits de la dreta, un per un.
Gira a la dreta
El següent nombre binari es gira 3 bits cap a la dreta:

La rotació es pot fer per un, dos, tres, quatre, etc.
Rorate Esquerra
El següent nombre binari es gira 3 posicions de bit cap a l'esquerra:

La rotació es pot fer per un, dos, tres, quatre, etc.
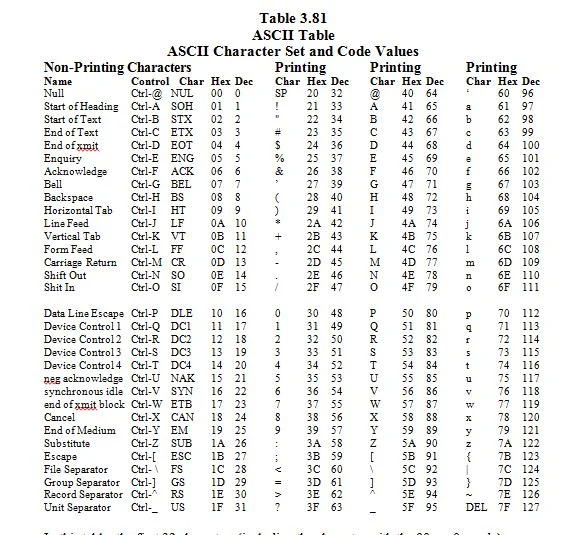
3.8 Conjunt de caràcters ASCII i els seus valors de codi
ASCII significa 'American (U.S.A) Standard Code for Information Interchange'. Imagineu un teclat amb 96 tecles. Aquest és un teclat ideal on les tecles de lletres majúscules són diferents de les tecles de lletres minúscules. Totes les altres tecles representen un caràcter que es troba en un teclat anglès (EUA). Els caràcters i els codis (números corresponents als caràcters) es mostren a continuació:
En aquesta taula, els primers 32 caràcters (inclòs el caràcter amb el 00 16 = 0 10 codi) són caràcters que no s'imprimeixen. Són personatges de control. No es veuen a la pantalla (monitor) on tot són iguals. Només tenen efectes. Parlem més sobre això més endavant.
La resta de caràcters són caràcters d'impressió; es veuen a la pantalla. Hi ha 128 caràcters ASCII. 2 7 = 128. 1,111,111 2 = 127 10 . El 7 en 2 7 significa 7 bits.
Ara, 1111111 2 + 1 2 és el mateix que:
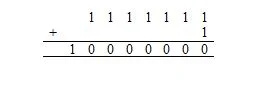
Aquí, 10.000.000 2 = 128 10 . N'hi ha 128 10 caràcters de la llista anterior (taula) de caràcters ASCII. Això inclou el caràcter nul, el codi del qual en base setze (hexadecimal) és 00, que equival a 0 en base deu.
Com que hi ha 128 caràcters en total, 128 menys 32 caràcters no imprimibles donen 96 caràcters d'impressió. En aquesta secció, se suposa que hi ha un teclat ideal amb 96 caràcters que són caràcters imprimibles. En aquest teclat ideal, les tecles dels caràcters anglesos majúscules són diferents de les tecles dels caràcters anglesos en minúscules.
Cada caràcter del teclat està representat per un nombre base dos de 7 bits que no es mostren a la llista. La lletra majúscula de 'N', per exemple, es representa amb els set bits 1001110 a la base 2. Per convertir 1001110 2 a la base 16, precediu-lo amb 0 i agrupeu el resultat en subgrups de quatre bits de la manera següent:
| 0100 | 1110 | 2 = | 4 | E | 16
Això és 01001110 2 = 4E 16 . Per convertir 4E 16 a la base deu, feu el següent:
4 x (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 10
A la dreta de 'N' a la llista (taula) hi ha el nombre hexadecimal de 4E i el nombre decimal de 78.
Com a altre exemple, el caràcter “[“ es representa amb els set bits 1011011 a la base 2. Per convertir 1011011 2 a la base 16, precediu-lo amb 0 i agrupeu el resultat en subgrups de quatre bits de la següent manera:
| 0101 | 1011 | 2 = | 5 | B | 16
Això és 01011011 2 = 5B 16 . Per convertir 5B16 a base deu, feu el següent:
5 x (16) 1 + B x (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 10
A la dreta de '[' a la llista (taula) hi ha el nombre hexadecimal de 5B i el nombre decimal de 91.
Com a exemple més, el caràcter del nombre decimal '5' es representa amb els set bits 0110101 a la base 2 i no 0000101 a la base 2. Per convertir 0110101 2 a la base 16, precediu-lo amb 0 i agrupeu el resultat en subgrups de quatre bits de la següent manera:
| 0011 | 0101 | 2 = | 5 | B | 16
Això és 00110101 2 = 35 16 . Per convertir 3516 a base deu, feu el següent:
3 x (16) 1 + 5 x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 10
A la dreta de '5' a la llista (taula) hi ha el nombre hexadecimal de 35 i el nombre decimal de 53.
Com que l'ordinador funciona en bytes, quan es prem una tecla del teclat ideal, s'envien vuit bits al microprocessador (placa mare). El teclat ideal és un perifèric que està separat de la unitat del sistema (base) de l'ordinador. Té un circuit electrònic (IC) que crea els set bits i el precedeix amb un zero abans d'enviar-lo a través del seu cable a la placa base de la unitat del sistema. Des del port d'entrada (circuit d'entrada) de la placa base, va al microprocessador que també es troba a la placa base. Des del microprocessador, passa a la memòria que també està instal·lada a la placa base.
Així, quan es prem la tecla 'N' del teclat ideal, vuit bits 01001110 es porten al microprocessador. Des del microprocessador, es porten a la memòria on romanen en una ubicació de memòria com a byte. El programador informàtic ha de tenir en compte que els vuit bits de 01001110 2 és el mateix que 4E 16 que és el mateix que 78 10 .
Quan es prem la tecla '[' del teclat ideal, es porten vuit bits 01011011 al microprocessador. Des del microprocessador, es porten a la memòria on romanen en una ubicació de memòria com a byte. El programador informàtic ha de tenir en compte que els vuit bits de 01011011 2 és el mateix que 5B 16 que és el mateix que 91 10 .
Quan es prem la tecla '5' del teclat ideal, com a caràcter i no com a nombre decimal, es porten vuit bits 00110101 al microprocessador. Des del microprocessador, es porten a la memòria on romanen en una ubicació de memòria com a byte. El programador informàtic ha de tenir en compte que els vuit bits de 00110101 2 és el mateix que 35 16 que és el mateix que 5310 10 .
Hi ha moments en què un programa s'està executant i espera que s'introdueixi el número decimal de 5 a l'ordinador. En aquesta situació, si es prem la tecla '5' del teclat ideal, encara es porta el codi de vuit bits de 00110101 al microprocessador. Com que el que es necessita és el número decimal de 5, i no el caràcter '5', un fragment de codi (programa curt) de la memòria utilitza el microprocessador per convertir el codi de caràcter de 00110101 en base dos al número de complement a dos 00000101. 2 abans d'enviar-lo a una ubicació de memòria com a byte de complement a dos. El programador informàtic ha de tenir en compte que 00000101 significa 5 10 a la base 2, i és diferent dels números de codi de 00110101 2 , 35 16 , i 53 10 que significa el caràcter de '5'. Per mostrar el número de complement de dos de 00000101 a la memòria, un altre programa curt ha de convertir 00000101 de la memòria a 00110101. És 00110101 que és el mateix que 35. 16 que és el mateix que 53 10 que es mostra al monitor (o imprès en un paper per la impressora).
3.9 Format de nombre de coma flotant
Un nombre sense part decimal és un nombre enter. El número 36 és un nombre enter. 36.375 no és un nombre enter. És un nombre decimal amb una part decimal. La part decimal de .375 és una fracció que és menor que 1.
36.375 s'interpreta en forma decimal com:
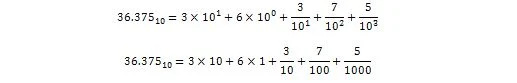
Ara:
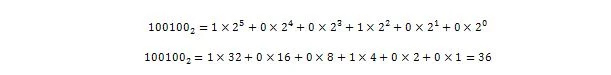
Així, 100100 2 = 3610, que és la part del nombre sencer de 36,375 10 .
Ara:
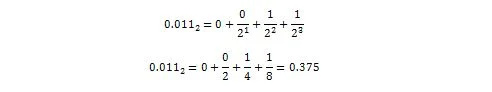
Així, 0,011 2 = 0.375 10 que és la part del número decimal de 36,375 10 .
∴ 36.375 10 = 100100.011 2
Dit d'una altra manera:
100100.011 2 = 36.375 10
Els nombres es representen a l'ordinador en base 2 i no en base 10, amb tot igual. Com que una cel·la d'un registre del microprocessador o una cel·la de la memòria només poden prendre 1 o 0, no hi ha espai per emmagatzemar un punt decimal. Això planteja un problema. Com a resolució, hi ha la representació de coma flotant de precisió única IEEE-754 de 32 bits i la representació de coma flotant de doble precisió IEEE-754 de 64 bits.
Format de nombre de coma flotant de 32 bits
El nombre 100100.0112 es pot expressar com:
100100.011 2 = 1.00100011 2 x 2 +5
El costat dret del símbol = es coneix en matemàtiques com la forma estàndard de base dues del costat esquerre de 100100.011 2 .
Ara, 00100011 d'1,00100011 2 a la part dreta del símbol =, sense el '1' anterior. i sense el 2 per a la base, s'anomena significat explícit. En aquest cas, el punt binari es pren cinc llocs a l'esquerra per tal de tenir l''1'. No confongueu entre punt decimal i punt binari. El punt binari és per a la base 2, mentre que el punt decimal és per a la base 10. L''1'. seguit de 00100011 a la part dreta del símbol =, sense el 2 per a la base, forma el significat veritable. Tanmateix, 1,00100011 s'anomena significat implícit.
Després del significat del costat dret hi ha 'x 2 +5 ” expressió. Amb aquesta expressió, el +5 s'anomena exponent. El signe més significa que el punt binari s'ha de moure cinc llocs cap endavant per tal d'estar en la seva posició original normal i 2 és la base per a la numeració. L'equació anterior es pot escriure al revés com:
1.00100011 2 x 2 +5 = 100100.011 2
Amb la representació de coma flotant de 32 bits, és '1.00100011 2 x 2 +5 ” que s'utilitza i no només “100100.011 2 ”. El 2 de la base no es registra. La representació de coma flotant de 32 bits per al '1.00100011 2 x 2 +5 ”, que és igual a 36.375 10 = 100100.011 2 , es mostra a la taula següent:

Hi ha posicions de 32 bits que estan numerades des de l'extrem dret, començant per 0. El primer bit de l'extrem esquerre és el bit de signe. Si el nombre és positiu, aquest bit és 0. Si el nombre és negatiu, aquest bit és 1 (-1 consta de dos caràcters i no es pot posar en cap cel·la). El 1.00100011 2 x 2 +5 que és igual a 36,375 10 que també és igual a 100100,011 2 és un nombre positiu. Per tant, el primer bit és 0.
Hi ha vuit posicions de bits per a l'exponent, començant des de la posició 30 fins a la posició 23, inclusivament. Tanmateix, l'exponent que s'escriu allà és 10000100 2 que és igual a 132 10 . L'exponent del nombre d'interès és en realitat +5 de la base de dos. Aleshores, què passa?
Ara, en el format de 32 bits, un exponent de 0 s'escriu com a 01111111 2 que és igual a 127 10 . El +5 10 és +101 2 . Per tant, en arribar a 10000100 2 a la part exponent de la taula, 101 2 s'ha afegit a 01111111 2 , corresponentment. Vol dir que 5 es van afegir a 127 per tenir 132 10 .
El significat, sense '1.', va baixar les posicions 22 a 15, ambdós inclosos. Tingueu en compte que l'1 de '1'. no s'ha indicat a la cadena de 32 bits. Mai s'indica: accepta-ho. La resta de cel·les fins a la posició 0 s'omplen de zeros.
Si l'exponent real és -5, llavors 5 es resta de 127 10 tenir 122 10 . Això correspon a restar 101 2 del 01111111 2 tenir 01111010 2 .
Amb tota la il·lustració anterior, el número +1 que és igual a 1,0 x 2 0 = 1,0 x 1 = 1,0 es representa com:

Tingueu en compte que el '1'. d'1,0 x 2 0 no s'indica en el format. Mai està indicat. La següent fracció mixta que surt positivament després de 1,0 és:

Observeu l'1 a l'extrem dret. Aquesta representació és el número:

La diferència entre 1,0000001192092896 i 1,0 és:
1.0000001192092896 – 1.0 = 0.0000001192092896
Els nombres amb parts decimals són fraccions mixtes. No totes les fraccions entre 1 10 i 2 10 es pot representar a l'ordinador. Es pot suposar que la bretxa fraccionària més petita entre els nombres mixtes consecutius amb el format de coma flotant de 32 bits és 0,0000001192092896. Espereu que l'interval de precisió doble sigui més petit. Consulteu la il·lustració següent.
En representar el nombre, 0,0 no segueix els arguments anteriors. La representació de 0.0 es declara i s'ha d'aprendre com a tal. Per representar 0,0, totes les cel·les del significat són 0 i totes les cel·les de l'exponent també són zero. El bit de signe pot ser 0 o 1. Malauradament, això dóna lloc a 0 positiu i 0 negatiu de la següent manera:

A la vida real, només hi ha un zero. El 0 positiu i el 0 negatiu no existeixen. No obstant això, 0 normalment es considera positiu. Aquí hi ha un 0 positiu i un 0 negatiu a causa d'aquesta descripció de format particular. La recta numèrica (vegeu més amunt) també pot tenir +0 i -0, però només existeix un zero.
Format de nombre de coma flotant de 64 bits
El format de coma flotant de 64 bits és similar al format de 32 bits, però amb les diferències següents:
- Hi ha 64 bits per representar un nombre.
- Després del bit de signe, hi ha 11 bits per al nombre exponent.
- El nombre exponent de l'índex zero (2 0 ) és 1023 10 = 01111111111 2 .
- Els onze bits són seguits per 52 bits per al significat explícit.
- Té un ventall de números més ampli que el format de 32 bits.
Tingueu en compte que el '1'. és a dir, al principi del significat encara no està inclòs entre els 64 bits, de la mateixa manera que no està inclòs entre els 32 bits per al format de 32 bits.
Una de les diferències més importants entre el format de 64 bits i el de 32 bits és que la diferència entre les fraccions mixtes consecutives en el format de 64 bits és menor que la del format de 32 bits.
En el format de 64 bits, l'interval (gap) entre 1,0 i la següent fracció mixta es pot calcular de la següent manera:
1.0 és
0 01111111111 00000000000000000000 00000000000 00000000000000000000 2
Això equival a l''1.', que no s'ha indicat a la cadena, multiplicat per 2 elevat a la potència (índex) 0 (amb l'exponent és 1023 10 = 01111111111 2 per 2 0 = 1). La corda fa 1,0 x 2 0 .
La següent fracció mixta superior a 1,0 és:
0 011111111111 00000000000000000000 00000000000 00000000000000000001 2
Això és equivalent a '1'. que no s'indica a la cadena, seguit de 51 zeros, i després 1, multiplicat per 2 elevat a la potència 0 (amb l'exponent és 1023 10 = 011111111112 2 per 2 0 = 1). Això és el mateix que:
+2 0 × (1 + 2− -52 ) ≈ 1.0000000000000002
El ≈ significa aproximadament igual a.
Ara:
1.0000000000000002 – 1.0 ≈ 0.0000000000000002
El valor d'interval corresponent per a un format de 32 bits és 0,0000001192092896 ≈ 0,00000012.
0,0000000000000002 és molt més petit que 0,00000012. Per tant, hi ha moltes més fraccions mixtes entre dos nombres enters consecutius (per exemple, 3 i 4) en el format de 64 bits que entre dos nombres enters consecutius en el format de 32 bits.
El nombre de fraccions mixtes entre dos nombres enters consecutius a la recta numèrica és infinit. Per tant, cap format (per exemple, 32 bits o 64 bits) pot proporcionar totes les fraccions mixtes entre dos nombres enters consecutius (nombres sencers). Com més petit sigui l'espai (interval) entre dos nombres enters consecutius proporcionats per un format (per exemple, 32 bits o 64 bits), més gran serà el nombre de fraccions mixtes entre els nombres enters consecutius (per a la recta numèrica).
Els motius pels quals el format de 64 bits es descriu com a precisió doble o superior, en comparació amb el format de 32 bits, són que l'interval entre dues fraccions mixtes consecutives limitades per dos nombres enters consecutius per al format de 64 bits és més petit que el de 32 bits corresponent. -Interval de format de bits. A més, hi ha més fraccions mixtes possibles entre dos nombres enters acotats per al format de 64 bits que no pas per al format de 32 bits.
Convertir una part decimal (fracció) d'un nombre decimal a una part binària
El 36,375 és un nombre decimal amb la part decimal de '.375'. La part decimal de '.375' és una fracció entre zero i un. El 0,5 de la base deu té el mateix valor que 1/2 de la base dos. El 0,5 10 que s'expressa amb l'expansió de base dos és:
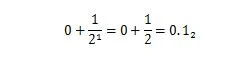
No és 0,101 2 que significa 0,625 10 . La part decimal d'un nombre decimal té la seva part binària equivalent per al nombre binari corresponent. Per tant, per convertir un nombre decimal com 36,375 10 a la base dos, convertiu 36 a binari i després convertiu .375 també a binari. A continuació, uneix els dos resultats amb el punt binari. Els mètodes per convertir les dues seccions són diferents. Com convertir un nombre enter decimal a base 2 s'explica al capítol 1.
Per convertir la fracció decimal a fracció binària, seguiu els passos següents:
- Multiplica la fracció decimal (part decimal) per 2. L'enter que resulta d'això és el primer dígit binari.
- Repetiu el pas anterior amb el resultat decimal fraccionari per obtenir el següent dígit binari.
- Continueu repetint el pas anterior fins que el resultat fraccionari decimal sigui .0000—.
Exemple: Converteix la part fraccionària de 36,375 10 a la part fraccionària equivalent a la base dos.
Solució:
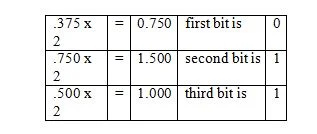
Tingueu en compte que en el tercer pas, .500 es va multiplicar per 2 i no per 1.500. La fracció binària corresponent es llegeix a l'última columna des de dalt. I per tant, el resultat següent és:
.375 10 = .011 2
Convertir una part binària (fracció) d'un nombre binari a una part decimal
Per aconseguir-ho, expandeix la fracció binària en potències recíproques de 2.
Exemple: Converteix la part fraccionària de 100100,011 2 a la part fraccionària equivalent en base deu.
Solució:
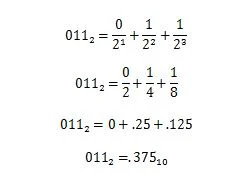
3.10 Prefixos de nombres en informàtica
A la vida normal, 1 quilo significa 1000 que s'abreuja en k (minúscula) com en 1kg. En informàtica, 1 quilo significa 2 10 = 1024, però s'abreuja en K (majúscula) com en 1Kbits. A la vida normal, 1 mega significa 1.000.000 que s'abreuja en M (majúscula) com en 1Mg. En informàtica, 1 mega significa 2 20 = 1,048,576 = 2 10 x 2 10 = 1024 x 1024 = 1.048.576 i encara s'abreuja en M (majúscula) com en 1 Mbits. A la vida normal, 1 giga significa que 1.000.000.000 s'abreuja en G (majúscula) com en 1Gg. En informàtica, 1 giga significa 2 30 = 1,073,741,824 = 2 10 x 2 10 x 2 10 = 1024 x 1024 x 1024 = 1.073.741.824 i encara s'abreuja en G (majúscula) com en 1 Gbits. La taula següent dóna el significat de quatre prefixos a la vida normal i a la informàtica:
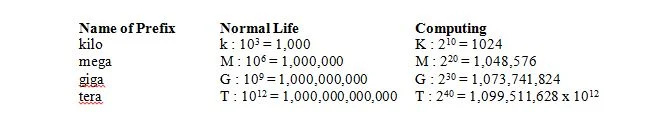
3.11 Problemes
Es recomana al lector que resolgui tots els problemes d'un capítol abans de passar al capítol següent.
- Dibuixa una recta numèrica amb nombres enters de -10 a +10.
- Afegiu els següents nombres binaris al complement de dos de 8 bits: 101010 2 i 1111 2 .
- Utilitzeu només l'enfocament del complement a dos en 8 bits per restar el nombre binari de 1111 2 a partir del nombre binari de 101010 2 .
- Troba el producte de 10110 2 x 1101 2 a la base dos.
- Dividiu 36.375 10 per 1000 10 en decimal i en binari, i comparar els resultats.
- Utilitzeu els 8 bits que trieu per il·lustrar els lògics AND, OR, XOR, Invert, Shift Right, Shift Left, Gire Right i Gire left. Cada byte ha de tenir una barreja d'1 i 0.
- a) Escriu el codi numèric del caràcter ASCII de zero en hexadecimal, binari i decimal.
b) Escriu el codi numèric del caràcter ASCII de “1” en hexadecimal, binari i decimal.
c) Escriu el codi numèric del caràcter ASCII de “A” en hexadecimal, binari i decimal.
d) Escriu el codi numèric del caràcter ASCII de “a” en hexadecimal, binari i decimal. - Converteix 49,49 10 a la base dos. Converteix el teu resultat al format de coma flotant IEEE de 32 bits.
- a) En què és diferent el format de coma flotant IEEE de 64 bits del format de 32 bits?
b) Doneu les dues raons relacionades per les quals el format de 64 bits es descriu com a precisió doble o superior a la
format de 32 bits.